Turbulent flow in a pipe

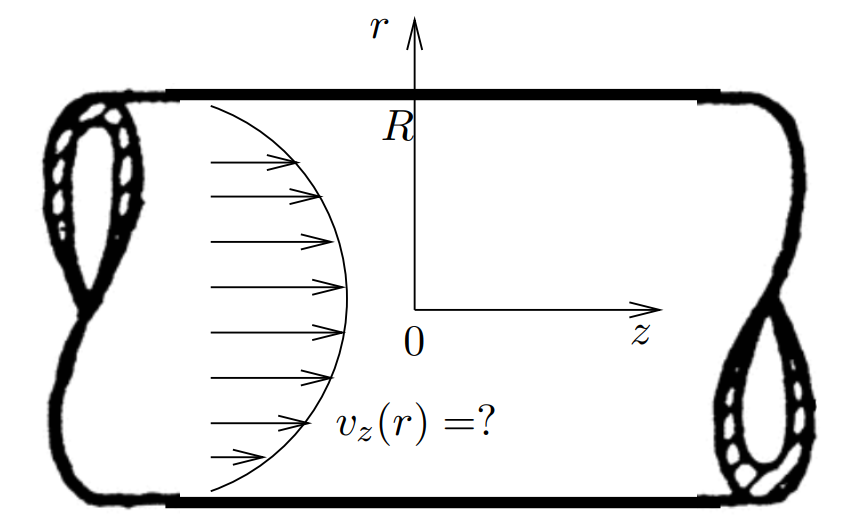
Problem

Derive a turbulent flow profile for an incompressible fluid with density $\rho$ and viscosity $\mu$ flowing in a long pipe with a radius $R$ in steady conditions.

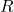
Solution

Let $\vec v$ be the time averaged velocity field, $p$ the modified pressure (i.e. pressure plus the contribution due to gravity $p=P+\rho\Phi_g$ ) and $\underline{\tau}$ the deviatoric stress tensor. The deviatoric stress tensor is a sum of viscous and turbulent parts $\underline{\tau}=\underline{\tau}_{vis}+\underline{\tau}_{tur}$ . With this, the Navier-Stokes equation can be written as

$\rho\frac{\partial \vec v}{\partial t} + \rho(\vec{v}\cdot\vec{\nabla})\vec{v} = -\vec{\nabla}p +\vec{\nabla}\cdot\underline{\tau}$

Let us simplify the equation by considering the polar coordinate system, $\vec{v}=(v_r,r_\theta,v_z)$
The following assumptions are considered: the flow is steady, so $\partial/\partial t=0$ , the flow is fully developed, so $\partial/\partial z=0$ and $v_r=v_\theta=0$ . After considering the assumptions, we observe that the left hand side of the Navier-Stokes equation is zero and on the right hand side the pressure gradient in the direction of the flow and a single component of the deviatoric stress tensor remain:

$\frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial}{\partial r}\left(r\tau_{rz}\right)$

Considering the above equation we observe that the left hand side can only depend on $z$ (since otherwise it must be zero due to the partial derivative) and by the same reasoning the right hand side can only depend on $r$ . The equation which features a term dependent on $z$ on one side and a term dependent on $r$ on the other can only be satisfied if both terms are constant. Since $p(z)$ and $\tau_{rz}(r)$ partial derivatives can be omitted

$\frac{dp}{dz}=\frac{1}{r}\frac{d}{dr}\left(r\tau_{rz}\right)$

We discovered, that the pressure drop in turbulent flow in a pipe does not change along the length of the pipe

$\frac{dp}{dz}=const.$

Solving for deviatoric stress

$\frac{d}{dr}\left(r\tau_{rz}\right)=r\frac{dp}{dz}$

$r\tau_{rz}=\frac{r^2}{2}\frac{dp}{dz}+A$

$\tau_{rz}=\frac{r}{2}\frac{dp}{dz}+\frac{A}{r}$

The constant $A=0$ since the deviatoric stress tensor is not infinite at the centre of the pipe ( $r=0$ ). This means

$\tau_{rz}=\frac{1}{2}\frac{dp}{dz}r$

the deviatoric stress is linearly proportional to the distance from the centre of the pipe $r$ , reaches the maximum value at the pipe surface ( $r=R$ ) and is equal to zero at the centre of the pipe.

Deviatoric stress is linearly proportional to the distance away from the centre of the pipe.

Experiments have shown that the turbulent stresses dominate the deviatoric stress tensor in the central region of the pipe and viscous stresses dominate the region close to the wall.

Let us first consider the center of the pipe, where $r\ll R$ . Using Prandtl’s mixing length model for turbulent stresses as the sole source of stress, we can write

$\rho(ay)^2\left(\frac{dv_z}{dy}\right)^2=\tau_0\frac{r}{R},$

where $\tau_0$ is the stress at the wall, $y=R-r$ is the distance from the wall and $a$ is the model constant. Simplifiying

$ay\frac{dv_z}{dy}=\sqrt{\frac{\tau_0}{\rho}}\sqrt{1-\frac{y}{R}}.$

At this point we introduce two quantities: the friction velocity and the turbulent length scale

$v^\star =\sqrt{\frac{\tau_0}{\rho}}, \qquad l^\star=\frac{\nu}{v^\star}$

wehre $\nu$ is the kinematic viscosity of the fluid. We use those to non-dimensionalize the velocity and distance

$v^+=\frac{v}{v^\star}, \qquad y^+=\frac{y}{l^\star}=\frac{v^\star}{\nu}y$

Using these nondimensional quantities we obtain

$dv_z^+=\frac{1}{a}\sqrt{1-\frac{y^+}{Re_\tau}}\frac{dy^+}{y^+}$

where $Re_\tau=v^\star R/\nu$ is the turbulent Reynolds number. Assuming we are not looking at the center of the pipe ( $y/R=y^+/Re_\tau\ll1$ ) we can simplify and solve

$dv_z^+=\frac{1}{a}\frac{dy^+}{y^+}$

$v_z^+=\frac{1}{a}\ln(y^+)+C$

Common choice for $a$ and $C$ that yields result comparable to experiment is

$v_z^+=2.5\ln(y^+)+5.5$

This equation is valid for $y^+>26$ and $y<R$ .

Secondly, we consider the region very close to the wall, where viscous diffusion dominates. There, we may assume that the deviatoric stress is constant and equal to the value at the wall. So

$\tau_{vis}=\tau_0=\mu\frac{dv_z}{dy}$

After integration and consideration that the velocity at the wall is zero (no-slip boundary condition) we can write

$v_z=\frac{\tau_0}{\mu}y$

or in plus units:

$v_z^+=y^+$

Turbulent flow profile in plus units. The green line shows an instantaneous profile obtained by direct numerical simulation for $Re_\tau=1000$ .

Turbulent flow profile in plus units. The green line shows an instantaneous profile obtained by direct numerical simulation for $Re_\tau=1000$ .

Leave a comment Cancel reply