Billiards ball collision

Problem

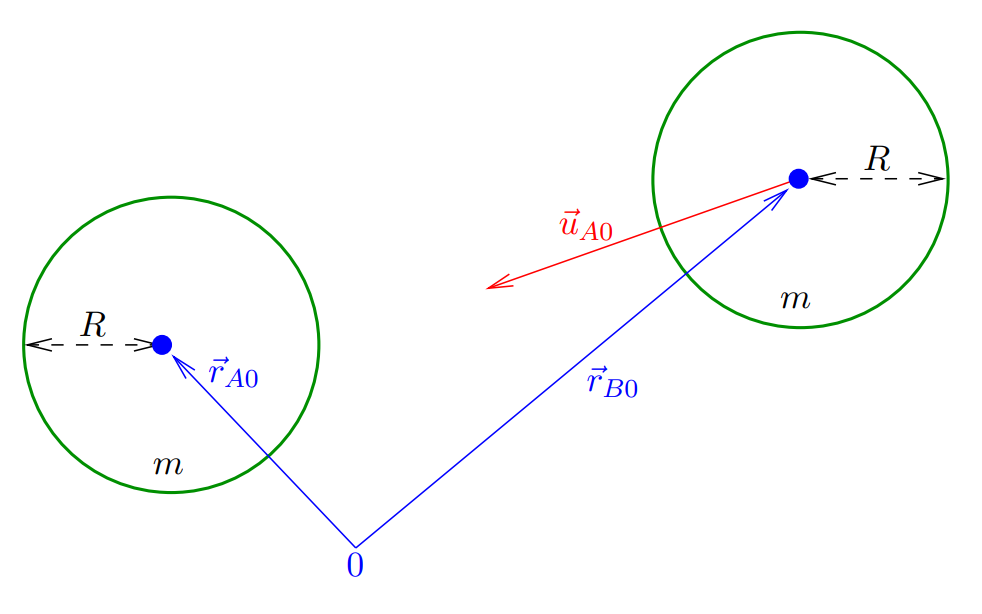
Let us consider two billiards balls on a very large pool table. Ball $A$ is stationary located at $\vec{r}_A$ , the other (ball $B$ ) is initially located at $\vec{r}_{B0}$ and has an initial velocity of $\vec{u}_{B0}$ and is on a collision course with the first ball. The friction and air resistance cause the ball to decelerate with $a=-\alpha u$ . Find the positions of both balls after collision when they stop moving. Ball are of equal size (radius $R$ ) and mass, the collision is elastic (coefficient of restitution is equal to one).

Data

– $\alpha$ , $R$
– $\vec{r}_{A0}$ , $\vec{r}_{B0}$ , $\vec{u}_{B0}$

The solution in a couple of steps

The velocity of the moving ball is

$\frac{d\vec{u}_B}{dt}=-\alpha \vec{u}_B$

Assuming the friction to be constant we may write

$\int_{\vec{u}_{B0}}^{\vec{u}_{B}}\frac{d\vec{u}_B}{\vec{u}_B}=-\alpha\int_0^tdt$

which leads to exponential decay of velocity with time

$\vec{u}_B(t)=\vec{u}_{B0}\exp(-\alpha t)$

Expressing the location of ball B with velocity is just another integral away

$\frac{d\vec{r}_B}{dt}=\vec{u}_B(t)=\vec{u}_{B0}\exp(-\alpha t)$

After integration we find, where ball $B$ will be located as a function of time

$\vec{r}_B(t)=\vec{r}_{B0}+\frac{\vec{u}_{B0}}{\alpha}\left(1-\exp(-\alpha t)\right)$

If no collision occurs, we can find the final position of the ball as

$\lim_{t\rightarrow\infty}\vec{r}_B(t)=\vec{r}_{B0}+\frac{\vec{u}_{B0}}{\alpha}$

Time of collision

In the next step we have to find the time at which collision occurs. Collision will happen when the distance between the balls is equal to $2R$ , i.e

$2R=|\vec{r}_B-\vec{r}_A|$

$(2R)^2= \left(r_{B0x}+\frac{u_{B0x}}{\alpha}(1-\exp(-\alpha t))-r_{A0x}\right)^2+$

$+ \left(r_{B0y}+\frac{u_{B0y}}{\alpha}(1-\exp(-\alpha t))-r_{A0y}\right)^2$

Temporarily naming $\beta = (1-\exp(-\alpha t))$ gives

$(2R)^2= \left(r_{B0x}+\frac{u_{B0x}}{\alpha}\beta-r_{A0x}\right)^2+ \left(r_{B0y}+\frac{u_{B0y}}{\alpha}\beta-r_{A0y}\right)^2$

Rearranging to a quadratic equation for $\beta$ :

$(r_{B0x}-r_{A0x})^2+(r_{B0y}-r_{A0y})^2-(2R)^2+$

$\left( 2(r_{B0x}-r_{A0x})\frac{u_{B0x}}{\alpha}+ 2(r_{B0y}-r_{A0y})\frac{ u_{B0y}}{\alpha} \right)\beta+$

$\left( \frac{u^2_{B0x}}{\alpha^2}+ \frac{u^2_{B0y}}{\alpha^2} \right)\beta^2=0 \nonumber$

Defining

$a = \frac{1}{\alpha^2} (u^2_{B0x}+u^2_{B0y})$

$c = (r_{B0x}-r_{A0x})^2+(r_{B0y}-r_{A0y})^2-(2R)^2$

$b = \frac{2}{\alpha}( (r_{B0x}-r_{A0x})u_{B0x} + (r_{B0y}-r_{A0y})u_{B0y} )$

helps us to use the quadratic formula to find the solutuion

$(1-\exp(-\alpha t)) = \beta = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$

and finally, the collision time is

$t=-\frac{1}{\alpha}\log\left(1-\frac{-b\pm\sqrt{b^2-4ac}}{2a}\right)$

There are two solutions for the collision time corresponding to the two points, where a line intersects a circle. For our case, the solution, which happens before is the correct one. As a side note, calculation of collision time may fail due to the fact the the square root or logarithm is undefined. When this happens, the collision does not occur (the ball is not on a collision course or stops before hitting the other ball)

At the moment of collision

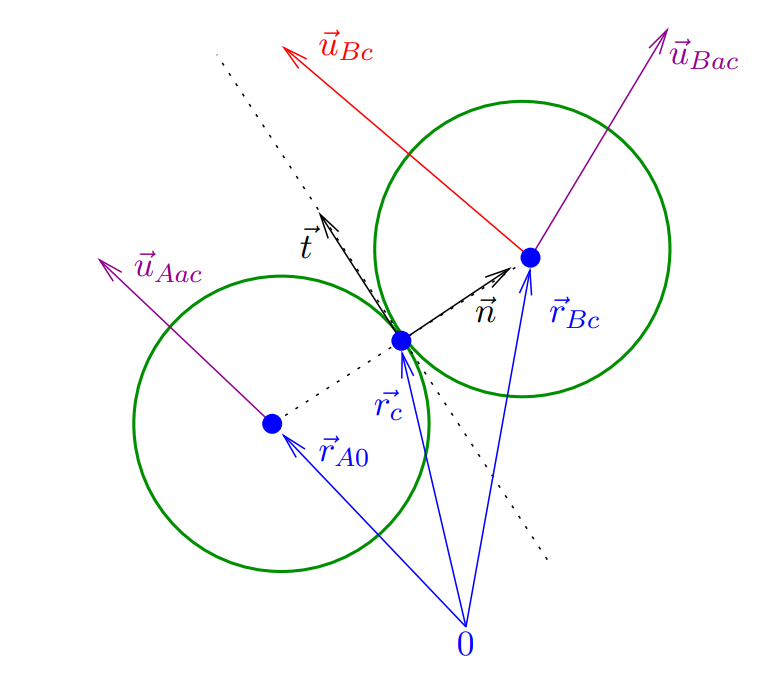
At the time of collision the ball $B$ is located at

$\vec{r}_{Bc}=\vec{r}_{B0}+\frac{\vec{u}_{B0}}{\alpha}\left(1-\exp(-\alpha t)\right)$

and it has a velocity of

$\vec{u}_{Bc}=\vec{u}_{B0}\exp(-\alpha t)$

First let us calculate a vector from the center of ball $A$ to the center of ball $B$ and normalize it:

$\vec{n}=\frac{\vec{r}_{Bc}-\vec{r}_{A0}}{|\vec{r}_{Bc}-\vec{r}_{A0}|}.$

The contact point is at

$\vec{r}_c=\vec{r}_{A0}+R\vec{n}.$

A tangent vector to the surfaces of the spheres from the contact point is $\vec{t}=(-n_y,n_x)$ .

We now decompose the velocity vectors of ball $B$ into normal and tangential directions (ball $A$ is stationary!)

$u_{B,t}=\vec{u}_{Bc}\cdot\vec{t},\qquad u_{B,n}=\vec{u}_{Bc}\cdot\vec{n}$

During the collision the tangential components are preserved

$u_{Aac,t}=0, \qquad u_{Bac,t}=u_{B,t}.$

In the normal direction, the momentum is conserved and since the collision is elastic with coefficient the restitution equal to one, the normal velocity is tranffered to balla $A$

$u_{Aac,n}=u_{B,n}, \qquad u_{Bac,n}=0.$

For a more general description of collision in 2D with an arbitrary velocity of both balls and any coefficient of restitution, see this post!

Afer collision

After collision, both balls are moving with velocity:

$\vec{u}_{Aac}=u_{Aac,t}\vec{t} + u_{Aac,n}\vec{n}$

$\vec{u}_{Bac}=u_{Bac,t}\vec{t} + u_{Bac,n}\vec{n}$

and they come to a stop at

$\vec{r}_{Af} = \vec{r}_{A0} + \frac{\vec{u}_{Aac}}{\alpha}$

$\vec{r}_{Bf} = \vec{r}_{Bc} + \frac{\vec{u}_{Bac}}{\alpha}$

Example

Consider the following data
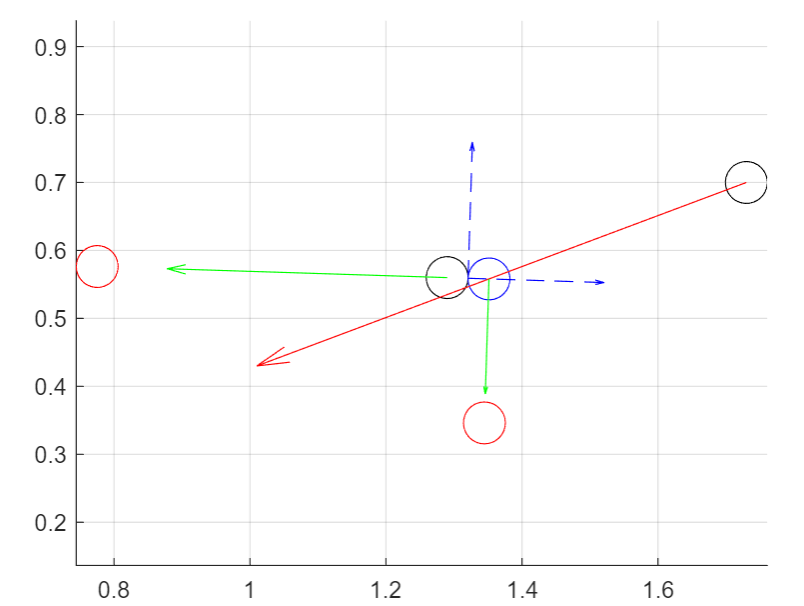
$\vec{r}_{A0}=(1.29,0.56)$ , $\vec{r}_{B0}=(1.73; 0.7)$ , $\vec{u}_{B0}=(-0.72, -0.27)$ , $\alpha=0.8$ , $R=0.03075$

Matlab solution

%
% Data
%
R=30.75/1000
alpha=0.8
rA0=[1.29; 0.56]
rB0=[1.73; 0.7]
uB0=[-0.72; -0.27]
%
% Collision time
%
a=(uB0(1)^2+uB0(2)^2)/alpha^2
b=2/alpha*( (rB0(1)-rA0(1))*uB0(1)+(rB0(2)-rA0(2))*uB0(2) )
c=(rB0(1)-rA0(1))^2 + (rB0(2)-rA0(2))^2 - (2*R)^2
dis=b^2-4*a*c
beta1=(-b+sqrt(dis))/(2*a)
beta2=(-b-sqrt(dis))/(2*a)
t1=-1/alpha*log(1-beta1)
t2=-1/alpha*log(1-beta2)
t=min(t1,t2)
%
% Ball B at collision time
%
rBc=rB0+uB0*(1-exp(-alpha*t))/alpha
uBc=uB0*exp(-alpha*t)
%
% Unit normal and tangent
%
n=(rBc-rA0)/norm(rBc-rA0);
t=[-n(2);n(1)];
%
% Collision point
%
rc=rA0+R*n;
%
% Normal and tangential velocity before collision
%
uAn=0
uBn=dot(uBc,n)
uAt=0
uBt=dot(uBc,t)
%
% Normal and tangential velocity after collision
%
uAtAC=uAt
uBtAC=uBt
uAnAC=uBn
uBnAC=uAn
%
% velocity after collision
%
uAac= uAtAC * t + uAnAC * n
uBac= uBtAC * t + uBnAC * n
%
% Final position
%
rAf=rA0+uAac/alpha
rBf=rBc+uBac/alpha
%
% Plot results
%
hold on
% spheres
circle(rA0(1),rA0(2),R,"black");
circle(rB0(1),rB0(2),R,"black");
circle(rBc(1),rBc(2),R,"blue");
circle(rAf(1),rAf(2),R,"red");
circle(rBf(1),rBf(2),R,"red");
% initial velocities
quiver(rB0(1),rB0(2),uB0(1),uB0(2),0,'-r')
% normal and tangent vectors
quiver(rc(1),rc(2),n(1)/5,n(2)/5,0,'--b')
quiver(rc(1),rc(2),t(1)/5,t(2)/5,0,'--b')
% velocity after collision
quiver(rA0(1),rA0(2),uAac(1),uAac(2),0,'-g')
quiver(rBc(1),rBc(2),uBac(1),uBac(2),0,'-g')
axis equal
grid on
hold off

function h = circle(x,y,r,color)
th = 0:pi/50:2*pi;
xunit = r * cos(th) + x;
yunit = r * sin(th) + y;
h = plot(xunit, yunit,color);
end

Matlab output:

Leave a comment Cancel reply