Laminar flow in a pipe

Problem

Derive a laminar flow profile for an incompressible fluid with density $\rho$ and viscosity $\mu$ flowing in a long pipe with a radius $R$ in steady conditions. Also, derive formulas for flow rate, maximal and average velocity!

Assumptions:
– the flow is laminar and steady,
– the fluid is incompressible,
– the flow is developed (i.e. the pipe is very long and we do not consider the section close to the inlet, $L\gg 0.12 \cdot R \cdot Re$ )
– the pipe is very long so the flow is axisymmetric

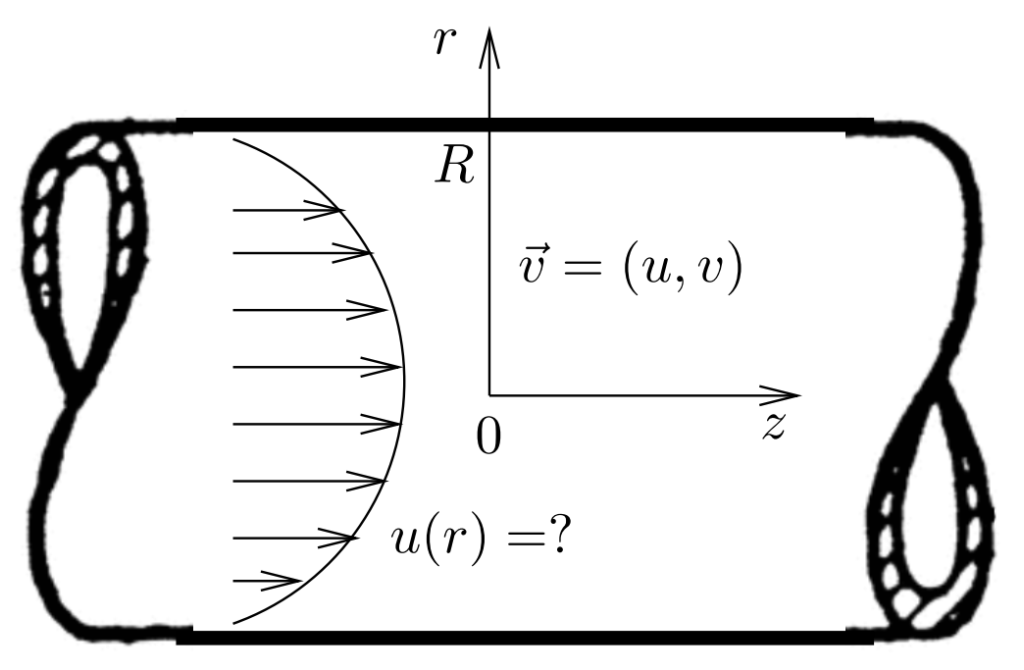
The solution, in a couple of steps:

We tackle the problem in polar coordinate system. The origin is at the center of the pipe, with $r$ axis pointing towards the perimeter and the $z$ axis along the pipe. The problem is axisymmetric, so the $\theta$ axis is irrelevant. The flow velocity has two components $\vec{v}=(u,v)$ , the $u$ component is the velocity along the pipe (along the $z$ axis) and the $v$ component is the velocity towards the perimeter of the pipe (along the $r$ axis).
The Navier-Stokes equations in this setting are: the continuity equation, the momentum transport equations in $z$ and in $r$ directions.

Consider the continuity equation:

The continuity equation for an incompressible fluid is:

$\frac{\partial u}{\partial z}+\frac{1}{r}\frac{\partial}{\partial r}(rv)=0.$

The first term is zero, since the flow is developed, so there are no changes in the velocity along the pipe, i.e. $\partial u/\partial z=0$ . From the second term, we then see

$rv=const.$

As the flow can not penetrate the pipe wall, we know $v(R)=0$ and so $Rv(R)=0$ . The means that the constant in the above equation is zero, and finally we conclude that $v=0$ everywhere.

The momentum equation across the pipe

The steady state momentum equation in $r$ direction is:

$\rho\left(u\frac{\partial v}{\partial z}+v\frac{\partial v}{\partial r}\right)= -\frac{\partial p}{\partial r} +\mu\left( \frac{\partial^2v}{\partial z^2}+\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial v}{\partial r}\right) \right).$

Since $v=0$ this equations simplifies to

$\frac{\partial p}{\partial r}=0,$

which means that the pressure is constant across the pipe and may only change along the pipe, i.e. $p=p(z)$ .

The momentum equation along the pipe

The steady state momentum equation in $z$ direction is:

$\rho\left(u\frac{\partial u}{\partial z}+v\frac{\partial u}{\partial r}\right)= -\frac{\partial p}{\partial z} +\mu\left( \frac{\partial^2u}{\partial z^2}+\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u}{\partial r}\right) \right).$

Taking into account $v=0$ and $\partial u/\partial z=0$ we simplify into

$\frac{\partial p}{\partial z} = \frac{\mu}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u}{\partial r}\right) .$

Since the left hand side of this equation depends solely on $r$ and the right hand side can only be a function of $z$ we conclude that the equation can only be satisfied if both sides are constant. This means that the pressure drop in the pipe is constant, i.e.

$\frac{\partial p}{\partial z} = -\frac{\Delta p}{L} = const.$

if $\Delta p$ is the pressure drop that occurs at a distance $L$ along the pipe. The minus sign comes from the fact that the pressure gradient is negative when pressure is decreasing in the direction of $z$ .

Solve the ordinary differential equation

Since we know, that the velocity $u$ depends only on $r$ , we can rewrite the steady state momentum equation in $z$ direction as a ordinary differential equation:

$\frac{d}{dr}\left(r\frac{du}{dr}\right) = -\frac{\Delta p}{\mu L}r$

We integrate twice and introduce two integration constants: $C_1$ and $C_2$ as

$r\frac{du}{dr} = -\frac{\Delta p}{\mu L}\frac{r^2}{2}+C_1$

$\frac{du}{dr} = -\frac{\Delta p}{\mu L}\frac{r}{2}+\frac{C_1}{r}$

$u = -\frac{\Delta p}{\mu L}\frac{r^2}{4}+C_1\ln(r)+C_2$

At this point we consider boundary conditions to determine the integration constants. Due to axisymmetry, we know that the maximal velocity will be at the center of the pipe at $r=0$ . This must be true, as momentum diffuses from the fluid into the pipe wall and since it does that axisymmetrically it must be true that the velocity is largest in the center of the pipe. In this way, momentum diffuses from the centre in all directions towards the walls. The velocity has an extrema at the center of the pipe

$\left.\frac{du}{dr}\right|_{r=0}=0.$

To satisfy this, it follows that $C_1=0$ . The second boundary condition comes from the fact that there is no slip between the fluid and the pipe wall. The fluid at the pipe wall is stationary, i.e.

$u(R)=0=-\frac{\Delta p}{\mu L}\frac{R^2}{4}+C_1\ln(R)+C_2.$

Since we already established that $C_1=0$ , we may work out that

$C_2=\frac{R^2\Delta p}{4\mu L}$

The Hagen-Poiseuille flow profile

Using the expressions for the integration constant, we can work out the Hagen-Poiseuille flow profile

$u(r)=\frac{R^2\Delta p}{4\mu L}\left(1-\left(\frac{r}{R}\right)^2\right)$

and the shear stress

$\tau_{rz}(r)=\mu\frac{du}{dr}=-\frac{\Delta p}{2L}r.$

The flow profile is parabolic with a maximum at the center of the pipe and velocity equal to zero at the pipe wall. The shear stress changes linearly from zero at the center of the pipe to the maximal value at the pipe wall.

The flow rate, the maximal velocity and the average velocity:

The maximal fluid velocity is at the center of the pipe, so:

$u_{max}=u(0)=\frac{R^2\Delta p}{4\mu L}.$

The flow rate can be calculated by means of integration across the pipe.

$\dot{V}=\int_A\vec{v}\cdot\vec{n}dA = \int_0^Ru(r)\cdot 2\pi r dr$

$\dot{V}= \frac{\pi R^2\Delta p}{2\mu L} \int_0^R\left(1-\left(\frac{r}{R}\right)^2\right) r dr$

Substituting $t=r/R$ and $dr=Rdt$ we obtain

$\dot{V}= \frac{\pi R^4\Delta p}{2\mu L} \int_0^1\left(1-t^2\right) dt$

The integral above evaluates to $1/4$ and we find an expression for the flow rate in a pipe:

$\dot{V}= \frac{\pi R^4\Delta p}{8\mu L}.$

We observe that the flow rate is linearly proportional to the pressure drop, scales inversely with fluid viscosity and is proportional to the radius to the power of four. This means, is one wants to pump the same amount of fluid per second in a pipe with half the diameter, one must provide 16 times larger pressure drop.

The average flow velocity is

$u_{ave}=\frac{\dot{V}}{A}=\frac{\dot{V}}{\pi R^2}=\frac{R^2\Delta p}{8\mu L}$

It is interesting to note, that the maximal velocity is twice as large as the average velocity

$u_{max}=2u_{ave}.$

The Darcy-Weisbach formula and the Darcy friction factor

Let us express the pressure drop in terms of the average velocity. Using the pipe diameter $D=2R$ and introducing the flow Reynolds number as $Re=\rho D u_{ave}/\mu$ we may write:

$\Delta p = \frac{8\mu L}{R^2}u_{ave} = \frac{16\mu }{R}u_{ave}\frac{L}{D} = \frac{32\rho }{ Re}u^2_{ave}\frac{L}{D}.$

A final rearrangement gives

$\Delta p = \frac{1}{2}\rho u^2_{ave} \cdot \frac{64}{ Re} \cdot \frac{L}{D}$

Here, the factor $64/Re$ is the Darcy friction factor. Expressing the pressure drop with head loss, i.e. $\Delta p = \rho g h_{loss}$ , we can write

$h_{loss} = \frac{u^2_{ave}}{2g} \cdot \frac{64}{ Re} \cdot \frac{L}{D},$

which is known as the Darcy-Weisbach formula.

Leave a comment Cancel reply