Heat transfer in a solid wall

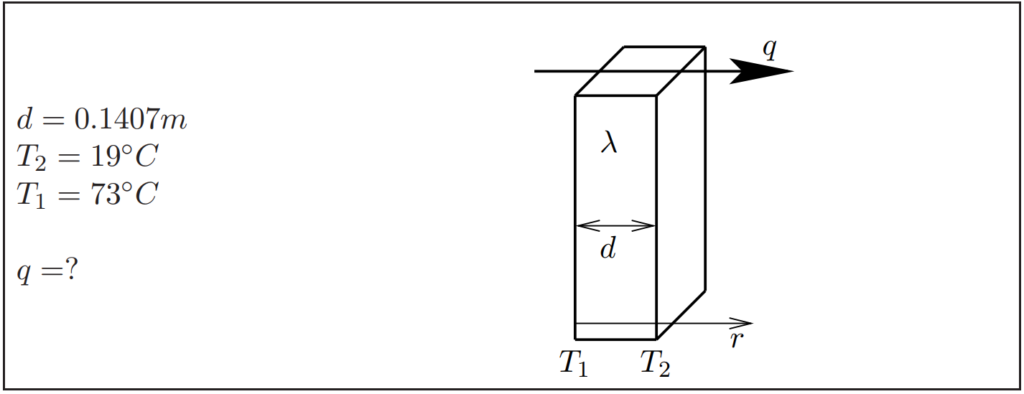
Problem

A beech board $14.07 ~ cm$ thick is heated to $19^\circ C$ on one side and to $73^\circ C$ on the other. Assuming steady one-dimensional conditions, determine the heat flux through it!

Data

Solution

The unsteady one-dimensional heat transfer equation is written as follows:

$\rho c_p\frac{\partial T}{\partial t}=\frac{1}{r^n}\frac{\partial}{\partial r}\left(r^n\lambda\frac{\partial T}{\partial r}\right)+I,$

where $\lambda$ is the heat conductivity, $\rho$ wood density, $c_p$ is the specific heat of the wood and $I$ are heat sources. When $n=0$ the equation is valid for planar geometry, with $n=1$ its valid for a cylinder and with $n=2$ its for spherical geometry.

For a wooden board we consider $n=0$ . Since we are considering steady state, temperature does not change and thus $\frac{\partial T}{\partial t}=0$ . At the same time, there are no heat sources in the wood, so $I=0$ . Furthermore, we assume that the wood is homogenous and that heat conductivity in the wood is constant, i..e indepenent of position and temperature. When looking up beech wood in an engineering handbook and find out its thermal conductivity is $\lambda=0.35~W/mK$ . These assumptions leed to simplification of the heat transfer equation to

$\frac{d^2T}{dr^2}=0.$

A general solution of the above equation is $T(r)=Ar+B$ . Constants $A$ and $B$ are calculated using known temperature on both sides. The boundary conditions are $T(0)=T_1$ and $T(d)=T_2$ .

Finally, we obtain the temperature distribution within the board:

$T(r)=T_1+\frac{T_2-T_1}{d}r.$

The heat flux is propotional to the temperature gradient

$\vec q=-\lambda\vec\nabla T$

Since we consider only one-dimensional heat transfer the gradient can be simplified to a derivative and the heat flux is a scalar quantity

$q=-\lambda\frac{dT}{dr}=-\lambda\frac{T_2-T_1}{d}=134.3~W/m^2.$

Leave a comment Cancel reply